(This is an expanded version of the 2nd part of a talk I gave last month. For the first part, see this post.)
Homotopical categories
The topic for this post is “homotopical categories”, and their role in algebraic geometry. I want to emphasize that I am very much in the process of learning about all these things, so this post is based more on interest and enthusiasm than actual knowledge. I hope to convey some of the main ideas and why they could be interesting, and come back to the details in many future posts, after having learned more. I apologize for not defining everything carefully, and for brushing the “stable” aspects of the theory, i.e. spectra and sheaves of spectra, under the carpet.
There are many different ways to speak of “homotopical categories”, and I only use this expression because I don’t know of a better thing to call them. The most well-known approach is the language of model categories, invented by Quillen and developed by many others. There are many excellent online introductions, for example Dwyer-Spalinski, Goerss-Schemmerhorn, and appendix A2 of Jacob Lurie’s book on higher topos theory, available on his webpage. Other languages are given by the many different approaches to higher categories; see the nLab page and the survey of Bergner. Still other languages include Segal categories, A-infinity categories, infinity-stacks, and homotopical categories in the precise sense of Dwyer-Hirschhorn-Kan-Smith.
Although I don’t want to go into the details of all these different homotopical/higher-categorical subtleties, I will try to list some of the basic features that “homotopical” categories typically have.
- A homotopical category should behave like a nice category of topological spaces.
- In particular, there should be a class of morphisms called weak equivalences, and:
- To any homotopical category
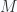 , one should be able to associate a “homotopy category”
, one should be able to associate a “homotopy category” 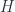 and a functor
and a functor  which is universal among functors sending weak equivalences to isomorphisms. Morally,
which is universal among functors sending weak equivalences to isomorphisms. Morally, 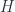 is obtained from
is obtained from 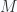 by “formally inverting the weak equivalences”.
by “formally inverting the weak equivalences”.
- A homotopical category should admit all limits and colimits, and also homotopy limits and homotopy colimits.
- A homotopical category should be enriched over some kind of spaces, i.e. for any two objects
 , the set
, the set  should be a “space” in some sense, for example a simplicial set, a topological space, or a chain complex of abelian groups.
should be a “space” in some sense, for example a simplicial set, a topological space, or a chain complex of abelian groups.
Simplicial objects
Before talking about algebraic geometry, we need to recall some “simplicial language”. The category 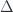 is defined as follows. Objects are the finite ordered sets of the form
is defined as follows. Objects are the finite ordered sets of the form ![[n]:= \{ 0,1,2, \ldots , n \}](https://s0.wp.com/latex.php?latex=%5Bn%5D%3A%3D+%5C%7B+0%2C1%2C2%2C+%5Cldots+%2C+n+%5C%7D&bg=fafcff&fg=2a2a2a&s=0&c=20201002) . Morphisms are order-preserving functions
. Morphisms are order-preserving functions ![[m] \to [n]](https://s0.wp.com/latex.php?latex=%5Bm%5D+%5Cto+%5Bn%5D&bg=fafcff&fg=2a2a2a&s=0&c=20201002) , i.e. functions such that
, i.e. functions such that 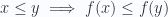 . If
. If 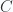 is any category, we define the category
is any category, we define the category  of simplicial
of simplicial 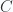 -objects to be the category in which the objects are the contravariant functors from
-objects to be the category in which the objects are the contravariant functors from 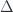 to
to 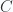 , and the morphisms are the natural transformations of functors. There is a functor from
, and the morphisms are the natural transformations of functors. There is a functor from 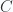 to
to  given by sending an object
given by sending an object  of
of 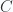 to the corresponding constant functor, i.e. the functor sending all objects to
to the corresponding constant functor, i.e. the functor sending all objects to  and all morphisms to the identity morphisms of
and all morphisms to the identity morphisms of  .
.
Some examples:
- Take
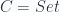 , the category of sets. The above construction gives us the category
, the category of sets. The above construction gives us the category  of simplicial sets. This category is “sort of the same as the category
of simplicial sets. This category is “sort of the same as the category 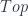 of topological spaces”. The precise statement is that there is a pair of adjoint functors which make
of topological spaces”. The precise statement is that there is a pair of adjoint functors which make 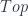 and
and into Quillen equivalent model categories; in particular, their homotopy categories are equivalent (as categories). For the purposes of algebraic topology, we can work with any of these categories. For example, we can define homotopy groups and various generalized homology and cohomology groups of a simplicial set. The inclusion of
into Quillen equivalent model categories; in particular, their homotopy categories are equivalent (as categories). For the purposes of algebraic topology, we can work with any of these categories. For example, we can define homotopy groups and various generalized homology and cohomology groups of a simplicial set. The inclusion of 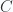 into
into  corresponds to viewing a set as a discrete topological space. A weak equivalence between two simplicial sets is a morphism inducing isomorphisms on all homotopy groups.
corresponds to viewing a set as a discrete topological space. A weak equivalence between two simplicial sets is a morphism inducing isomorphisms on all homotopy groups.
- Take
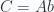 , the category of abelian groups. There is a forgetful functor from
, the category of abelian groups. There is a forgetful functor from 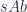 to the category
to the category  , induced by the forgetful functor from
, induced by the forgetful functor from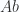 to
to . The Dold-Kan correspondence tells us that there is an equivalence between
. The Dold-Kan correspondence tells us that there is an equivalence between 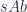 and the category of (non-negatively graded) chain complexes of abelian groups. Under this equivalence, homotopy groups of a simplicial abelian group correspond to homology groups of a chain complex.
and the category of (non-negatively graded) chain complexes of abelian groups. Under this equivalence, homotopy groups of a simplicial abelian group correspond to homology groups of a chain complex.
- Take
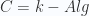 , the category of
, the category of -algebras for a commutative ring
-algebras for a commutative ring . Then there is some kind of Dold-Kan correspondence between simplicial algebras and DG-algebras. See Schwede-Shipley for precise statements.
. Then there is some kind of Dold-Kan correspondence between simplicial algebras and DG-algebras. See Schwede-Shipley for precise statements.
- Take
 , the category of sheaves of sets on some topological space or site. Then
, the category of sheaves of sets on some topological space or site. Then  is the category of simplicial sheaves. This category can also be viewed as the category of sheaves of simplicial sets on the site. Any category of simplicial sheaves is a “homotopical category” (I am not making this precise here). For example, one way of defining weak equivalences is to say that a morphism of simplicial sheaves is a weak equivalence iff it induces weak equivalences of simplicial sets on all stalks.
is the category of simplicial sheaves. This category can also be viewed as the category of sheaves of simplicial sets on the site. Any category of simplicial sheaves is a “homotopical category” (I am not making this precise here). For example, one way of defining weak equivalences is to say that a morphism of simplicial sheaves is a weak equivalence iff it induces weak equivalences of simplicial sets on all stalks.
Homotopical categories in algebraic geometry
Now to algebraic geometry. Through a few examples I want to argue that homotopical categories (in particular categories of simplicial sheaves) provide a useful and natural setting for certain aspects of algebraic geometry.
Firstly, let’s consider the general problem of viewing a cohomology theory as a representable functor. In algebraic topology, the Brown representability theorem says that any generalized cohomology group is representable, when viewed as a functor on the homotopy category  of topological spaces. In other words, there is a space
of topological spaces. In other words, there is a space 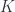 such that the cohomology of a space
such that the cohomology of a space  is given by
is given by 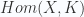 , where the
, where the 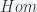 is taken in the homotopy category. Examples include the Eilenberg-MacLane spaces
is taken in the homotopy category. Examples include the Eilenberg-MacLane spaces 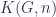 , which represent the singular cohomology groups
, which represent the singular cohomology groups  , and the space
, and the space  , which represents K-theory. The existence of a long exact sequence relating the cohomology groups for various
, which represents K-theory. The existence of a long exact sequence relating the cohomology groups for various  corresponds to the fact that the different Eilenberg-MacLane spaces fit together to form a so called spectrum. The Brown representability theorem is best expressed using the language of spectra, i.e. stable homotopy theory, but I want to postpone a discussion of this to a future post. An interesting aspect of Brown representability for singular cohomology is that by identifying the coefficient group
corresponds to the fact that the different Eilenberg-MacLane spaces fit together to form a so called spectrum. The Brown representability theorem is best expressed using the language of spectra, i.e. stable homotopy theory, but I want to postpone a discussion of this to a future post. An interesting aspect of Brown representability for singular cohomology is that by identifying the coefficient group 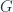 with the corresponding Eilenberg-MacLane space, the two arguments of a singular cohomology group
with the corresponding Eilenberg-MacLane space, the two arguments of a singular cohomology group  , namely the space
, namely the space  and the coefficient group
and the coefficient group 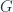 , suddenly are on equal footing. By this I mean that they both live in the same category of topological spaces, rather than in the two separate worlds of topological spaces and abelian groups, respectively.
, suddenly are on equal footing. By this I mean that they both live in the same category of topological spaces, rather than in the two separate worlds of topological spaces and abelian groups, respectively.
In classical algebraic geometry, there is no analogue of Brown representability. Most cohomology theories are of the form 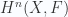 , where
, where  is some kind of variety, and
is some kind of variety, and 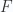 is a sheaf of abelian groups. One may ask if there is a way to express such a cohomology group as a representable functor. In order to obtain a picture parallell to the topological picture above, a necessary requirement is to have a homotopical category in which the variety
is a sheaf of abelian groups. One may ask if there is a way to express such a cohomology group as a representable functor. In order to obtain a picture parallell to the topological picture above, a necessary requirement is to have a homotopical category in which the variety  and the sheaf
and the sheaf 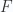 both live as objects, “on equal footing”. One possibility for such a category is some category of simplicial sheaves. In order to explain how this works, let us fix some category
both live as objects, “on equal footing”. One possibility for such a category is some category of simplicial sheaves. In order to explain how this works, let us fix some category 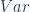 of varieties, for example the category smooth varieties over some base field
of varieties, for example the category smooth varieties over some base field  . Let us also fix some Grothendieck topology on this category, for example the Zariski topology, the Nisnevich topology, the etale topology, or some flat topology. This defines a site, and we can speak of sheaves on this site, i.e. contravariant functors on
. Let us also fix some Grothendieck topology on this category, for example the Zariski topology, the Nisnevich topology, the etale topology, or some flat topology. This defines a site, and we can speak of sheaves on this site, i.e. contravariant functors on 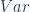 , satisfying a “glueing” or “descent” condition with respect to the given topology.
, satisfying a “glueing” or “descent” condition with respect to the given topology.
Since Grothendieck, we are familiar with the idea of identifying a variety with the sheaf of sets that it represents, by the Yoneda embedding. We mentioned earlier that for any category 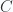 , there is a functor
, there is a functor  . Taking
. Taking 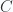 to be the category of sheaves of sets, we get a functor from sheaves of sets to simplicial sheaves. In particular, any variety can be viewed as a simplicial sheaf, by composing the Yoneda embedding with the canonical functor from sheaves of sets to simplicial sheaves.
to be the category of sheaves of sets, we get a functor from sheaves of sets to simplicial sheaves. In particular, any variety can be viewed as a simplicial sheaf, by composing the Yoneda embedding with the canonical functor from sheaves of sets to simplicial sheaves.
We also want to show that a sheaf of abelian groups can be viewed as a simplicial sheaf. We can regard any abelian group as a chain complex, by placing it in degree zero, and placing the zero group in all other degrees. This gives an embedding of the category of abelian groups into the category of chain complexes, and by composing with the Dold-Kan equivalence we get a functor from abelian groups to simplicial sets. This induces a functor from sheaves of abelian groups to simplicial sheaves. More generally, any complex of sheaves of abelian groups can be viewed as a simplicial sheaf.
Now one could hope for an analogue of Brown representability, namely that the sheaf cohomology group 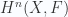 could be expressed as
could be expressed as  , where the Hom is taken in the homotopy category of simplicial sheaves. It seems to be the case that something along these lines should be true. For example, this nLab page on cohomology seems to imply that all forms of cohomology should be of this form, at least sheaf cohomology groups of the type just described. Also, Hornbostel has proved a Brown representability theorem in the setting of motivic homotopy theory.
, where the Hom is taken in the homotopy category of simplicial sheaves. It seems to be the case that something along these lines should be true. For example, this nLab page on cohomology seems to imply that all forms of cohomology should be of this form, at least sheaf cohomology groups of the type just described. Also, Hornbostel has proved a Brown representability theorem in the setting of motivic homotopy theory.
There are many other phenomena in algebraic geometry which also seem to indicate that categories of simplicial sheaves might be more natural to study than the smaller categories of schemes and varieties we typically consider. Some examples (longer explanations of these will have to wait until future posts):
- It seems to be the case that almost any geometric object generalizing the concept of a variety can be thought of as a simplicial sheaf. Examples: Simplicial varieties, stacks, algebraic spaces.
- Deligne’s groundbreaking work on Hodge theory in the 70s (see Hodge II and Hodge III) uses in a crucial way that the singular cohomology of a complex variety can be defined on the larger category of simplicial varieties. Simplicial varieties are special cases of simplicial sheaves, and I believe it should be true that functors on simplicial varieties can be extended to simplicial sheaves.
- Simplicial varieties/schemes also pop up naturally in other settings. For example, Huber and Kings need K-theory of simplicial schemes for their work on the motivic polylogarithm.
- As already indicated, simplicial sheaves appears to be the most natural domain of definition for many different kinds of cohomology theories.
- Morel and Voevodsky’s A1-homotopy theory (also known as motivic homotopy theory) is based on categories of simplicial sheaves for the Nisnevich topology.
- Brown showed that Quillen’s algebraic K-theory can be thought of as “generalized sheaf cohomology”, where the coefficients is no longer a sheaf of abelian groups, but a simplicial sheaf.
- The work of Thomason relating algebraic K-theory and etale cohomology uses the language of simplicial sheaves.
- Simplicial sheaves provide a natural language for “resolutions”. For example, it gives a unified picture of the two methods for computing sheaf cohomology: Cech cohomology and injective resolutions.
- Simplicial sheaves seems to be the most natural language for descent theory.
- Toen‘s work on higher stacks can be formulated in terms of simplicial sheaves.
- Homotopy categories of simplicial sheaves can be thought of a generalization of the more classical derived categories of sheaves. The homotopical point of view seems to clarify some unpleasant aspects of the classical theory of triangulated categories.
See also the nLab entry on motivation for sheaves, cohomology, and higher stacks.
Questions
I hope to come back to many of these examples in detail. For now, I just want to list a few questions which I find intriguing.
- To define a category of simplicial sheaves, we must choose a Grothendieck topology. How does this choice affect the properties of the category we obtain? Morel and Voevodsky work with the Nisnevich topology, Huber and Kings work with the Zariski topology, and Toen (at least sometimes) works with some flat topology. For some purposes, it seems to be the case that we don’t need a topology at all, instead we can just work with simplicial presheaves. What is the role of the Grothendieck topology?
- Most of the above examples are developed for varieties over a base field of characteristic zero. Based on the above, it seems reasonable to believe that simplicial sheaves are useful in this case, but what if the base scheme is field of characteristic p, a local ring, a Dedekind domain, or something even more general? Is it the case that simplicial sheaves is the most natural language for understanding cohomology theories for arithmetic schemes, such as schemes which are flat and of finite type over
 ? Are simplicial sheaves important in number theory/Arakelov theory/geometry over the field with one element? What are the obstacles to “doing homotopy theory over an arithmetic base”?
? Are simplicial sheaves important in number theory/Arakelov theory/geometry over the field with one element? What are the obstacles to “doing homotopy theory over an arithmetic base”?
Obviously I hope that there will be interesting answers to these questions, but I am still completely in the dark as to what these answers might be.