What is geometry?
Posted by Andreas Holmstrom on April 20, 2009
(This is an extended set of notes for Part 1 of a talk I gave a few days ago at the Young Researchers in Mathematics conference in Cambridge. Part 2 will be posted soon.)
What is geometry? What is a “space”? When is an object “geometric”? Everyone would agree that a manifold is a geometric object, and similarly for a CW complex, and probably also for a scheme. But what about a group – is it a geometric object? What about a noncommutative ring? These and other mathematical objects form categories – but when should a category be regarded as a geometric category?
The question “What is geometry” is of course very naive, but I believe it is still of some interest. First of all, it is interesting from a historical point of view to look at the answers given at various points in history, and how our idea of geometry has developed over time. Secondly, when developing new forms of geometry, where sometimes even the fundamental definitions and constructions are not completely in place, it could possibly be helpful to have spent some time reflecting on what geometry really is. The new forms of geometry I have in mind include Arakelov geometry, geometry over , derived algebraic geometry, and various forms of noncommutative geometry. Thirdly, one would like to understand for what kinds of objects one can define “cohomology”. For example, we can define various forms of cohomology for manifolds, schemes, Lie algebras, associative algebras, groups, rigid analytic spaces,
-algebras, ring spectra, categories, stacks, operads, and many other things. What exactly do these objects have in common?
What follows is a list of suggestions for conceptual answers to the question “What is geometry?”. Of course the answers are complementary, each of them capturing some particular aspect of what geometry is.
1. For a very long time, geometry was the same thing as Euclidean geometry, and to say or think something else was almost unheard of. Only in the 19th century did Western mathematicians begin to realize that there could actually be other forms of geometry.
2. The famous Erlangen program, formulated by Klein in 1872, gave a unification of the various types of geometry existing at the time, focusing on the notion of symmetry, and on properties invariant under symmetry groups. These ideas had a huge impact on the development of Lie theory and various other subjects in geometry and physics.
3. There is something called “Cartan geometries” (developed by Élie Cartan), which appears to be a further generalization of the Erlangen program, including Riemannian geometry in the picture. I have not found a good online source, but there is a book by Sharpe.
4. One important way of approaching geometry is to shift focus from the geometric object to some set of functions on the object. For example, one could replace a topological space by the ring of continuous complex-valued functions on the space, or replace an algebraic variety with the ring of polynomial functions on the variety. In many cases, this process gives an equivalence of categories. This approach is the standard way of introducing Grothendieck‘s schemes, and is also the basic idea of noncommutative geometry.
5. Closely related to the previous item is the idea of defining geometry as the study of locally ringed spaces. In their really nice introduction to algebraic geometry, Demazure and Gabriel define a geometric space to be a locally ringed space.
6. One could “define” a geometric category as a category admitting an interesting functor to (the homotopy category of topological spaces). Some examples to motivate this approach: For categories of (well-behaved) topological spaces with some extra structures, e.g. smooth manifolds, there is a forgetful functor to
and hence to
. For the category of groups, and more generally the category of small categories, we have the classifying space functor. For the category of (non-negatively graded) chain complexes of abelian groups, we have the Dold-Kan correspondence, which gives a functor to simplicial abelian groups and hence to Hot (more about this example in Part 2 of the talk).
7. Another way of “defining” a geometric category could be: A category admitting some notion of cohomology. The problem with this definition is of course that it is hard to define what exactly we mean by cohomology, but it should be a functor to some abelian category, producing long exact sequences and spectral sequences in ways similar to what we observe in topology and algebraic geometry.
8. There are various approaches to “homotopical categories”, and we could define geometry as the study of these categories. The most well-known approach is probably Quillen’s notion of model categories. There are many other approaches and languages as well, for example various notions of infinity-categories, homotopical categories in the sense of Dwyer-Hirschhorn-Kan-Smith, higher stacks, Segal categories, simplicial sheaves, simplicial categories, -categories, and more. I will say more about this in Part 2 of the talk.
9. In the 60s, Lawvere developed the concept of a “theory”. As a special case, there is something called a “geometric theory”, which could maybe serve as a way to define what geometry is. For more about this, see the online book by Barr and Wells, in particular sections 4.5 and 8.3.
10. Some people would argue that everything is geometry.
Some remarks: There are probably many other approaches to answering the question we started with. It seems to me that a good definition of geometry should (1) allow for noncommutative structures, and (2) agree with the principle that everything algebraic is also geometric.
In Part 2 of the talk (to be posted soon!) I will say something about point no 8, homotopical categories, and try to show that they can be useful in algebraic geometry.
D. Eppstein said
There’s a danger in this approach of false syllogisms of the form “I like geometry. I like cohomology. Therefore, geometry is cohomology.”
Novice said
Reading an introductory book on Algebraic Topology, say Hatcher’s or Spanier’s, one gets the impression that homotopy came into the scene as a weaker notion than homeomorphism, as a tool to attack the too difficult problem of classifying topological spaces.
That being so, how did homotopy theory get so much importance as implied by your post? As in your implication that all of geometry boils down to homotopy theory?
homotopical said
Hi, thanks for the comment. I did not mean to say that all of geometry boils down to homotopy theory (or to cohomology), but rather that for some purposes, the perspective of homotopy theory simplifies certain things which are difficult without this perspective. As I wrote, I am sure there are many other ways of answering the question of what geometry is, and each of them (including any homotopy-theoretic approach) will only capture certain aspects of what geometry is. Also, even if it would be the case that a given “geometric category” could be embedded in a homotopical category, that would of course not solve all the questions we had about the original category (in principle, it is conceivable that it might not help us at all).
Regarding the impression given by Hatcher, I think you are completely right. However, those books are intended to cover algebraic topology only, and it seems to be the case that the language and tools of homotopy theory are applicable to a much larger range of objects, in particular objects from algebraic geometry. I will expand on these ideas in the next post, and try to be more clear about what I mean.
Novice said
One question about 6, on a terminology from algebra.
It is about, “a forgetful functor to Top and hence to Hot”..
I have never seen a precise definition of a forgetful functor in literature. In easy situations like manifolds to Top or Top to Sets, I can understand it concretely and I skip it. But it would be nice to know what a forgetful functor is, when the target category is Hot. Do you have a reference where I can check in?
homotopical said
Just to avoid any possible confusion about 6: The forgetful functor goes from manifolds to Top, and composing this functor with the canonical functor from Top to Hot gives a functor from manifolds to Hot, which I don’t think can be viewed as a forgetful functor, since it is not faithful.
I have never seen a precise definition of forgetful functor, just a lot of examples, like you. The only place I have seen giving some sort of definition is the online book by Adamek, Herrlich and Strecker, where they define “concrete category” on the first page of chapter 5. In their definition, a forgetful functor is part of the structure of a concrete category, and the only requirement on the functor is that it is faithful. If we take this as a definition, my guess is that forgetful functors to Hot are not very useful, since most interesting functors to Hot are non-faithful.
There is a discussion about the precise definition of forgetful functor at the Wikipedia talk page, and from this, and the main article itself, it seems to be the case that there is actually no precise definition of forgetful functor. There is an interesting distinction though between three kinds of forgetful functors, namely those “removing axioms”, those “removing predicates”, and those “removing types”. I don’t know enough about logic to understand this, but there are some clarifying examples as well in the article.
As an side remark, I believe it is true that Hot itself is an example of a category which is not a concrete category over Set, i.e. Hot is not a category of “sets with additional structure”.
Novice said
This was helpful.
For 7, 8 and also your clarification on 6, one is left with a queasy feeling that some logical difficulty might arise in the use of categories. Was this problem settled to satisfaction?
homotopical said
All of these points were a bit vague, since I have not given a precise definition of “interesting functor”, or “cohomology”, or “homotopical category”. However, I don’t think there is any deep logical difficulty lurking because of the use of categories. What exactly do you find worrying? None of these points are really meant as a definition in the mathematical sense, but rather as metamathematical and naive observations that many categories we usually think of as part of geometry satisfy these properties. I hope I can post the next blog post tonight, and that should at least make point no 8 a bit clearer.
Novice said
The logical difficulties aren’t the essential part and they may be a distraction from the geometric questions in mind. But, it feels like cheating when you are not really sure that there are no foundational problems, even if the general opinion is that everything could be worked out well.
For instance, the notion of infinity categories itself raises set-theoretical doubts in mind. Other doubtful points could be like, “embedding all geometric categories and functors into homotopic categories”, “the category of all categories”(even if you use small categories, there will be situations where there are difficulties.
I am sorry to distract you from the main topic, which is geometry.
Novice said
Could you explain a little bit about the “Beyond Part 3” lecture series? I do not have much idea of Cambridge and would love to know a little bit. The website link you have given seems to be not working for the last two days.
homotopical said
Oh, I hadn’t noticed that the site is down. It used to be a webpage for the conference, but I am guessing that they are reshaping it, turning it into a general networking and resource page for young mathematicians. I believe the new page is supposed to appear eventually at the new address http://www.youngresearchersinmaths.org/ (if this doesn’t work, try to google young researchers in maths).
The conference was a workshop for graduate students and recent PhDs in mathematics. The name Beyond Part III was a bit misleading since it gives the impression that it was only for people who have done Part III in Cambridge. This course, also known as Certificate of Advanced Study in Mathematics, is a sort of one-year Master’s course, attracting students from all over the world. More info about Part III here, and about maths in Cambridge in general here. Is there anything specific you would like to know?
Novice said
1. Is a foreign student welcome to participate? Do they give funding? What are the criteria to get invited?
2. You are Andreas Holmstrom?
3. Do the students talk on their work? Is giving a talk necessary for participation?
And I suppose, one must wait until the next year Spring, for the next event?
homotopical said
1. Oh yes, very much so. I am foreign myself 🙂 and many came from foreign universities as well. I am not sure about funding but I believed there was quite a lot of support available. All graduate students in mathematics were welcome.
2. Yes
3. Yes, students talked about their work, but this was not at all necessary for participation. I am not sure if/when there will be a huge event like this again. My guess is that it will happen again but not next year. However, every now and then there are smaller events on particular subareas of maths.
Now the conference site is live again.
Novice said
Thanks for all the info. I had never heard about this type of events in Cambridge; henceforth I will keep my ears tuned.
You should post more on your ideas on geometry, for the benefit of others. Although a mere novice, even I can see that you often address fundamental issues.
homotopical said
Update: I talked to one of the main organisers a few days ago, and he said that there would probably be another big event already next year. So look out for more information…
Novice said
Thanks. Looking at things optimistically, at one of such events I would run into you and then I’ll be sure to introduce myself; “Hi, I’m Novice”, etc.
Novice said
I checked up a bit on homotopy stuff after seeing your blog post. Can you enlighten me with a blog post on “brave new” theories? If this is not possible, a personal communication will do.
homotopical said
It will take some time before I get around to writing about brave new rings and related things. However, here are some links. I’ll probably come back to this at some point in the future – it’s a very exciting subject about which I hope to learn more.
A project description on brave new rings.
An introduction to the subject, from an Oberwolfach workshop.
Peter May: Brave new worlds in stable homotopy theory.
Greenlees: First steps in brave new commutative algebra.
Novice said
Could you please explain a bit about the meaning of the phrase “brave new”? I do not know the intricacies of language. But such strong expressions of optimism as “brave new” invokes a slight distrust in me.
homotopical said
All I know is that Waldhausen coined the term “brave new ring” in the 80s. The phrase comes from the famous novel Brave New World of Huxley. Of course one can discuss whether it is appropriate to use this term in mathematics, but I don’t think it is meant as a very strong expression of optimism. I interpret it at just an easy-to-remember name for a type of “rings” which were certainly new at the time, and maybe also “brave” in some sense.
Novice said
I checked wikipedia on the said novel. The world described therein is certainly quirky and the phrase seems to have a jocular content as well. Due to my naivete at first I took the phrase to mean great optimism.
How important are brave new rings in homotopy theory? Since you are doing homotopy theory and you still haven’t fully looked into it yet, it certainly can’t be absolutely essential for the subject.
homotopical said
Unfortunately I am not in a position to answer the question about how important brave new rings are. My interest in homotopy theory is a relatively recent thing, so I lack a lot of background. You have to ask someone with more experience in the subject.
Novice said
Now, getting back to the blog post. I see from your homepage that you have read Tate’s thesis. So you have changed from arithmetical investigations to geometric investigations.
And there is the implication in one of your points that everything could be geometry. Is it possible to present a hardcore arithmetical topic such as the reciprocity investigations of Gauss, Eisenstein etc., as geometry? Since you’ve done etale cohomology etc., I hope you are qualified to answer.
Novice said
Btw I would be very interested in having a look at your write-up on Tate’s thesis. The link in your homepage is not working.
homotopical said
I could send it to you by email. Can I use the gmail address you are giving when you post your comments? I could also send you more references about the reciprocity stuff if you are interested.
homotopical said
That’s a very interesting question, I’m sorry about the delay in replying. I was meaning to write a longer reply, but I simply don’t have the time at the moment, so I will just give a brief answer.
If you only look at classical reciprocity laws (Gauss etc), which are unified in class field theory (CFT), the subject doesn’t look very “geometric”, although it is possible to use group cohomology to prove many of the main results of CFT (See e.g. Cassels and Fröhlich: Algebraic number theory).
However, there are several generalizations of reciprocity laws/CFT which in different ways are more geometric than the classical stuff. Here is a brief list of such generalizations, and there are probably others as well.
1. The Langlands program. There are many parts to this, including local Langlands (in zero and positive characteristic), global Langlands (in zero and positive characteristic), geometric Langlands, and p-adic Langlands in the sense of Breuil and others. Local and global Langlands are generalizations of local and global CFT. For example, for K a number field, global Langlands for the group GL(n) relates (conjecturally)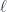 -adic representations of the absolute Galois group of K (which are de Rham at
-adic representations of the absolute Galois group of K (which are de Rham at 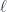 and almost everywhere unramified) to so called algebraic automorphic representation of GL(n,A), where A is the adele ring of the number field. For n = 1 we recover the statements of global class field theory, and similarly for local Langlands and local CFT. A lot is known about local Langlands, and the proofs we have use a lot of algebraic geometry, see for example Harris and Taylor: The geometry and cohomology of some simple Shimura varieties. When it comes to global Langlands, Lafforgue got the Fields medal for GL(n) in the function field case (char p) while in the number field case (char zero) there is only very limited progress. Without knowing much about Lafforgue’s work, it seems reasonable to think that he was able to do the function field case precisely because things can be interpreted geometrically, in terms of curves over finite fields, while in the number field case, one of the reasons things are hard is that we don’t have any “geometry over the field with one element”, so the geometric arguments are not available.
and almost everywhere unramified) to so called algebraic automorphic representation of GL(n,A), where A is the adele ring of the number field. For n = 1 we recover the statements of global class field theory, and similarly for local Langlands and local CFT. A lot is known about local Langlands, and the proofs we have use a lot of algebraic geometry, see for example Harris and Taylor: The geometry and cohomology of some simple Shimura varieties. When it comes to global Langlands, Lafforgue got the Fields medal for GL(n) in the function field case (char p) while in the number field case (char zero) there is only very limited progress. Without knowing much about Lafforgue’s work, it seems reasonable to think that he was able to do the function field case precisely because things can be interpreted geometrically, in terms of curves over finite fields, while in the number field case, one of the reasons things are hard is that we don’t have any “geometry over the field with one element”, so the geometric arguments are not available.
2. It is is possible to formulate “reciprocity laws” for arithmetic schemes, see for example Wiesend: Class field theory for arithmetic schemes, and older work by Kato and Saito. Link: http://www.springerlink.com/content/p225753t146h2533/
3. Kato also has a notion of “explicit reciprocity laws”, see for example http://www.numdam.org/item?id=BSMF_1991__119_4_397_0 but I don’t know much about this.
4. There might be a connection between local CFT/local Langlands with homotopy theory, hinted at the last page of this survey of Morava: http://front.math.ucdavis.edu/0707.3216
All in all, I think there is good reason to say that there is a lot of geometry in the subject of “generalized” reciprocity laws. Hope this gives at least a partial answer to your question.
Novice said
Hmm. It would appear that the char-p Langlands is the work of Drinfel’d(according to wikipedia), and indeed the Geometric Langlands is due to him.
It would seem that reciprocity is captured in some representation theoretic statement a la Langlands, and this is supposed to be geometrical. I have heard representation theorists proposing in a broad sense that “everything is representation theory”. When I just remarked the “everything is geometry” statement to someone, I got the reply that from the abstract point of view of category theory, pretty much anything could be made into pretty much anything else.
Yeah, it is enough to use the e-mail address in the comments. However it would be nice if you don’t reveal it to others(so that I can continue to be an unidentified novice).
Homotopical categories and simplicial sheaves « Motivic stuff said
[…] Posted by homotopical on May 20, 2009 (This is an expanded version the 2nd part of a talk I gave last month. For the first part, see this post.) […]
Thomas said
New on arxiv: A focused modernization of Sophus Lie’s brilliant writings about the foundations of geometry that every contemporary geometer should have at least once a look at. Translated, updated, commented..
Novice said
This was useful. Thanks for recommending it.